Už delší dobu jsem zvažoval, zda v rámci série Zaostřeno na blue-chips nevěnovat jeden příspěvek pohledu na to, jak tu vlastně některé čísla tvořím a odvozuji. Žádost jednoho ze čtenářů o totéž mi signalizuje, že je skutečně načase. Podívejme se tedy na to, jakou logiku má zde uplatňovaný pohled. Dostaneme se i k tomu, proč jsou poslední roky z valuačního hlediska dost výjimečné a proč žijeme v době, kdy „jen nebe je limitem“ (jen trochu jsem tím zapřeháněl).
Při odhadu hodnoty akcie nás zajímá, jakou hotovost nám bude přinášet. Používáme tak odhady budoucích dividend (takový vrabec v hrsti), nebo tzv. volného cash flow na vlastní jmění FCFE. To je často spíše holubem na střeše. Je to CF, které v principu patří akcionářům, mělo by být vyplaceno, či zhodnoceno odpovídající návratností, ale tato teorie mnohdy naráží na řadu překážek behaviorálních i jiných. Dobře je to patrné v současné době, kdy firmy drží hromadu hotovosti. Omezme se zde nyní na dividendy. Nejjednodušším způsobem, jak odhadnout hodnotu akcie, je předpoklad, že dividendy současného období (roku) porostou nějakým stabilním tempem (aproximujeme tak krátkodobé výkyvy a změny do dlouhého pohledu).
Máme – li obrázek o dividendách, už nám stačí jen určit požadovanou návratnost a máme odhad hodnoty akcie. Od roku 1962 totiž můžeme používat Gordonův vzorec, který říká, že hodnota akcie V je rovna dividendě z tohoto roku (jeho konce) D dělené rozdílem mezi požadovanou návratností R a očekávaným růstem dividend D. Pokud je dividenda 10, požadovaná návratnost 10 % a růst dividend nulový (jde v podstatě o nekonečný rizikový dluhopis), hodnota akcie je 100 (10 děleno 10 %). Na efektivním trhu by pak měla cena akcie P odpovídat V.
V následující tabulce je příklad s požadovanou návratností ve výši 7 %, očekávaným růstem dividend ve výši 4 – 6,5 % a dividendou t+1 ve výši 1. Využitím gordonova vzorce odvodíme, že pokud je G 4 %, hodnota akcie (a její cena) je 33,3 (1/(7% - 4%)). Pokud je G 6,5 %, hodnota se vyšplhá na 200.
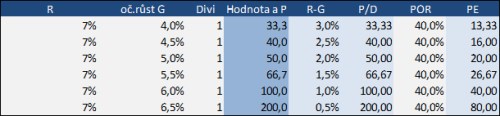
V sloupci R – G je rozdíl
mezi požadovanou návratností a očekávaným růstem. Jak ukazují prezentované
hodnoty a ještě lépe jejich zobrazení v grafu, odhad hodnoty na snižování
tohoto rozdílu reaguje nelineárně – stále citlivěji. To samé platí o valuačních
násobcích – v tabulce je poměr ceny a dividendy PD (protože dividenda je
1, je PD stejné jako odhad hodnoty). S předpokladem 40 % výplatního poměru
POR (dividendy/zisky) můžeme pro demonstraci ukázat i PE (poslední sloupec
tabulky).

Ve zdejší sérii často pracuji
s tím, že odvodím požadovanou návratnost, cenu akcie známe a pokusím se
odvodit očekávaný růst dividend (či FCFE). Logika je jednoduchá – pokud by byl
cenou akcie implikovaný růst příliš vysoko (nízko), cena akcie je příliš vysoko
(nízko) Ono „příliš“ je samozřejmě subjektivním názorem, který lze odvodit na
základě řady porovnání a úvah (růst odvětví, ostatních firem, místní ekonomiky,
globální ekonomiky, historický růst CF ...). Jsem ale přesvědčen, že taková
základní rozborka ceny akcie na požadovanou návratnost a implikovaný růst
poskytuje většinou lepší vhled do věci, než třeba porovnávání násobků. O pouhém
povídkovém investování nemluvě.
Pokud je například cena akcie
100, současná dividenda 10 a požadovaná návratnost 10 %, tato cena akcie
implikuje nulový růst dividend. S tím už se dá pracovat – je to
realistické s ohledem na to, jak se vyvíjí firma, odvětví, ekonomika?
Nejednou může být podobný pohled rozumný kompromis mezi příliš zjednodušujícími
násobky a časově příliš náročným kompletním DCF. Tedy kompromis sloužící třeba
jako síto pro určení toho, čemu by mohlo být vhodné se věnovat více.
Jak určit onu požadovanou
návratnost R? I když má nejednu mouchu, králem je zde model CAPM. Ten říká, že
R je u daného aktiva rovno bezrizikovému výnosu a rizikové prémii. Riziková
prémie je pak dána tím, jaká je prémie u celého trhu a jaká je rizikovost
aktiva relativně k trhu. U akcií se v praxi nejčastěji používají
výnosy desetiletých vládních dluhopisů jako bezrizikový výnos, tržní prémie
akciového trhu MRP a tzv. beta, která ukazuje citlivost pohybu akcie na pohyb
celého trhu. Zjistit bezrizikové výnosy je bezproblematické, u bety to je
složitější (závisí na období, rozdílech mezi minulostí a budoucností, způsobu
měření ...). MRP je nejproblematičtější, protože jí nelze přímo pozorovat a
musíme se proto spoléhat na odvozování ze současných cen a valuací, či
z historických trendů, průměrů ... Podle „Market Risk Premium used in 88
countries in 2014: a survey with 8,228 answers“ je nyní v průměru
používaná MRP v USA na 5,4 %. Já ve zdejších úvahách už nějaký čas (po
opadnutí posledního velkého risk-off) používám pro USA 5,5 %.
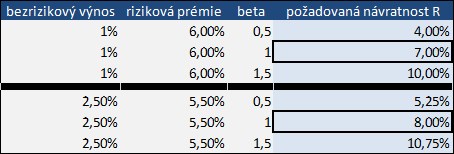
Pár příkladů odvození R: První
z následujících tabulek ukazuje výpočet odhadovaných návratností pro akcie
na německém trhu, druhá tabulka je pro USA. V Německu je výnos dlouhých
vládních dluhopisů na 1 %, MRP zde dejme o 0,5 procentního bodu nad MRP
v USA – tedy na 6 %. Pokud má společnost betu 0,5 (rizikovost k trhu
poloviční) je u ní požadovaná návratnost na 4 % (1 % + 0,5 * 6 %). U akcie
s betou 1 (a u celého trhu) je německé R na 7 %, u akcie s betou 1,5
je R 10 %. Obdobně můžeme postupovat u amerického trhu. Tam je vyšší
bezrizikový výnos, ale menší prémie. R u celého trhu je pak o procentní bod
výše než na německém trhu.
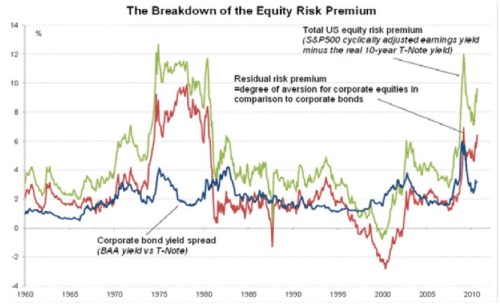
Celkově jsou dnes požadované návratnosti na vyspělých trzích dost nízko. Platí to zejména o srovnání s obdobími, kdy byly bezrizikové výnosy mnohem výše a to samé platilo o rizikových prémiích. Podle následujícího grafu byla například MRP na vrcholu poslední krize u 12 %, nad 10 % byla i v druhé polovině sedmdesátých let, kdy výnosy vládních dluhopisů převyšovaly 8 %. Požadovaná návratnost u US trhu tak během těchto období rostla vysoko nad 15 %. To se samozřejmě projevilo na cenách a valuacích a na rozdílech mezi R a G.
Proč je pro dnešní valuace někdy
jen nebe limitem? Protože se v plné síle projevuje onen exponenciální
efekt rozdílu mezi požadovanou návratností a růstem. Jsme ve výjimečném období,
kdy jsou bezrizikové výnosy velmi nízko, protože ekonomika je relativě utlumena
(USA), či hodně utlumena (eurozóna). Centrální banky v tom i přes
převažující mínění hlavní roli nehrají. Zároveň se ale výrazně zmenšila
volatilita, opadla velká averze k riziku a klesly rizikové prémie.
Požadovaná návratnost je tak celkově velmi nízko. Růstový výhled ekonomiky není
nic moc, firmy si ale nevedou špatně, jejich zisky většinou dále poměrně silně
rostou (diskuse „globalizace vs. roboti“).
Jsme tak v bodě, kdy je R a
G dost blízko sebe a každé další snížení tohoto rozdílu má (doposud mělo)
exponenciální dopad na ceny a valuace. Tento dopad je přitom fundamentálně
v pořádku. Stejně tak by ale byl v pořádku prudký pokles valuací daný
byť jen mírným zvětšením rozdílu R – G (růstem rizika, poklesem růstu). Můžeme
uvažovat o tom, že vlastně jde o jeden z mechanismů, kdy je klid (nízké
rizikové prémie) základem pro volatilitu budoucna a naopak.
Jak moc je situace „vážná“?
Vezměme například US sektor zdravotní péče. Jde o defenzívu s relativně
nízkou požadovanou návratností. Pětiletý výhled nyní podle konsenzu říká, že
zisky porostou ročně asi o 12 %. I kdyby byla požadovaná návratnost kolem 8 %
(rizikovost stejná jako u celého trhu), R – G je zde záporné. Zde není ani nebe
limitem – smysl má pouze detailnější DCF a i to bude díky blízkosti R a
skutečně dlouhodobého G generovat relativně vysoké hodnoty a násobky.
Každá kapka „vody“ ve formě
poklesu bezrizikových sazeb a/nebo poklesu rizikových prémií je nyní dost
cítit. Stejně tak ale bude cítit větší sucho. Nepropadejme ale panice – uvedené
mimo jiné ukazuje, že pokud je růst bezrizikových výnosů (zvyšování sazeb)
vyvažováno poklesem rizikových prémií (R je stabilní), či zvyšováním tempa
růstu (R – G je stabilní), pacient je propouštěn z šipky, protože se mu
daří lépe.
Pozn.: Jiří Soustružník je aktivní investor a
témata, o nichž píše, mohou souviset s jeho investicemi. Jeho sloupky
nejsou poskytovány jako investiční doporučení. Autor je externím
spolupracovníkem Patrie, jeho názory se nemusí vždy shodovat s názorem
společnosti.