Co riskuji při podniknutí investice do akcií Unipetrolu, ČEZ, vládních dluhopisů, nemovitosti ...? Riziko/nejistota - protipól toho, jaké zhodnocení investice očekávám, musí být součástí zvažování každé investiční strategie; rozdíl mezi hráčem a investorem je v jejich averzi vůči riziku. Investor posuzuje své výnosy vždy v kontextu rizika, které podstoupil. Předpoklad přímé úměry mezi rizikem a požadovaným výnosem je tak, zdá se, aplikovatelný pro většinu lidí, to alespoň je-li velikost investice nezanedbatelná ve srovnání s jejich celkovým majetkem. Zatímco s relativně malými částkami si lidé i pohrají, větší objemy jejich majetku radši investují. Jak tedy hodnotit úspěšnost investice v kontextu výnos-riziko? Po připomenutí základních měřítek rizika aplikovatelných zejména pro akciové trhy se v tomto článku podíváme na jednoduché užití VaR - value at risk. Ta, jak uvidíme, při kvantifikaci rizika jednoduchým způsobem spojuje jak čisté ukazatele rizikovosti, tak očekávanou výnosnost a dává zajímavou charakteristiku investice. Ač je tento ukazatel typický zejména pro risk management bank, pojišťoven a jim podobných institucí se složitými, na trh často navázanými portfolii aktiv, jeho základní princip je aplikovatelný i na běžné investice, včetně investic společností do projektů, reálných aktiv, apod. (podobně jako princip oceňování opcí).
CAPM, APT, Alfa a Sharp
Bereme-li v úvahu celkové riziko investice, kvantifikujeme ho většinou s pomocí směrodatné odchylky předpokládaných výnosů. Možnost diverzifikace portfolia snižuje toto celkové riziko na jeho systematickou část. I proto je dnes zřejmě nejpoužívanějším konceptem kvantifikujícím vztah mezi požadovanou mírou návratnosti a rizikem akcie CAPM, založený na teorii portfolia. Jeho klíčovým ukazatelem je zde již několikrát diskutovaná beta akcie (indikátor systematického rizika). Většina kritiky CAPM má svůj původ v tom, že samotná teorie portfolia je odvozena v rámci uzavřeného, neoklasického modelu ekonomiky, který je sice dobrým myšlenkovým rámcem pro posouzení určitých jevů v reálném světě, zdaleka ale není dostačující. Kritika je do značné míry zaměřená i na jeho nedostatečnou reflexi toho, že faktorů, které ovlivňují výnos akcie je více, než její citlivost na trh a návratnost trhu. To dalo základ multifaktorovým modelům, jako je např. APT. Jejich principem je definice několika faktorů určujících návratnost akcií a určení citlivostí (bet) akcie na každý takový faktor. Tento princip bere v úvahu opět pouze systematické riziko charakterizované betou (betami v případě multifaktorovým modelů). Ačkoliv princip rozdělení celkového rizika na systematické a nesystematické má elegantní teoretické zdůvodnění, není málo investorů, kteří minimálně někdy berou v úvahu stále riziko celkové (tedy nejen jeho systematickou část). V principu by tak měli činit všichni, kteří nemají dobře diverzifikované portfolio alespoň z několika desítek akcií.
Výše uvedené implikuje jeden z možných pohledů na úspěšnost investora v dimenzích riziko-výnos. Toto je reflektované v tzv. Jensenově alfě, která je definována jako realizovaná návratnost investice (potrfolia) mínus návratnost požadovaná (v rámci CAPM dána Rrf + beta*MRP) - nejde tedy o nic jiného, než o to, kolik investor vydělal nad, nebo pod, požadovanou míru návratnosti určenou za pomocí CAPM (alternativně APT). Jinak řečeno, nakolik investor překročil náklad investovaného kapitálu.
Sharpův poměr je pak měřítkem úspěšnosti investora, které je v principu definované jako jeho dosažený výnos upravený o riziko. Ukazuje, jaký byl výnos investora upravený o riziko, konkrétně výnos nad bezrizikovou investici dělený volatilitou jeho portfolia (jde o anualizované hodnoty, volatilita je anualizovaná denní standardní odchylka procentuálních změn hodnoty portfolia). Interpretace (tzn. posouzení úspěšnosti) výsledku investice na základě výše uvedeného poměru je samozřejmě silně subjektivní. Na základě zkušeností je např. někdy uváděno, že u neprofesionálních investorů je úspěchem překročení hodnoty 1 (v delším období). V tomto případě je návratnost portfolia nad bezrizikovou sazbu rovná volatilitě.
VaR
Value at Risk je absolutní měřítko rizika, které při daných předpokladech indikuje velikost možné ztráty na investici v daném období. Investuje-li např. investor do akcií a jeho roční 90% VaR je 10 000 korun, znamená to, že v průměru "v jednom roce z deseti" ztratí na této investici více než 10 000. Toto pak může (na stejné bázi, tj. tato ztráta relativně k investici) porovnat s investicemi do jiných akcií, popř. aktiv a zvážit, zda při předpokládaném výnosu těchto alternativ je dané riziko přijatelné. Předpokládám-li např. u dvou alternativ stejné zhodnocení (např. při stejné velikosti investice do obou ve velikosti 100 000 se zhodnotí o 10 % ročně), radši si vyberu to, která má 90% VaR 10 000, než tu, která má 90% VaR 20 000 (tzn. tu, která "ztratí v jednom roce z deseti" 10,000 místo 20,000).
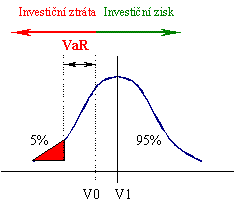
Pro kvantifikaci VaR je nutno odhadnout následující - jaké bude nejpravděpodobnější zhodnocení investice (hodnota v čase 1 mínus hodnota v čase 0: V1 - V0) a jak je charakterizováno celé pravděpodobnostní rozdělení budoucí hodnoty této investice (tvar, směrodatná odchylka). Pro standardní rozdělení a 95% VaR je uvedené znázorněno graficky:
 Zdroj: Patria Finance Zdroj: Patria Finance
|
VaR je v tomto případě rovno: X * sm.odch. + (V1 - V0). Faktor X odráží to, s jakou pravděpodobností při odhadu VaR pracujeme (např. pro 90 % je tento roven 1,282). Nejde zde tedy o nic jiného než o odhad maximální ztráty při dané pravděpodobnosti (X*sm.odch), snížený o předpokládané zhodnocení portfolia (V1 - V0). Čím větší směrodatná odchylka, tím větší možná ztráta. Čím větší předpokládané zhodnocení, tím menší ztráta.
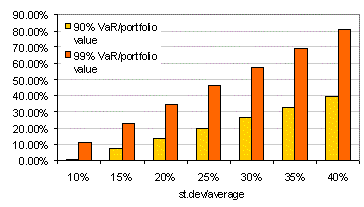
Je tedy možné provést kalkulaci VaR pro různé směrodatné odchylky imaginárního portfolia/investice. Např. investice o hodnotě 100 předpokládá roční návratnost 12 % (kvantifikovaná např. na základě CAPM). Podívejme se na to, jak je tato ohrožena ve smyslu maximální možné ztráty. Dejme tomu, že směrodatná odchylka možných výnosů jde od relativně malého rizika 10 % průměru (do rozmezí definovaného jednou sm.odch. u tohoto rozdělení padne 68,2 % očekávaných hodnot) až po velkých 40 % průměru - osa x.
Zdroj: Patria Finance
|
Tmavě oranžové hodnoty interpretujeme následovně - např. pro první platí, že v průměru v 1 roce ze sta (při 99% VaR) by u dané investice s poměrem sm.odch./průměr 10 % (osa x) ztratil investor více než cca. 10 % podniknuté investice (inkasoval by 90 po investování 100 na začátku roku). Světle oranžové hodnoty interpretujeme - např. pro poslední hodnotu platí, že v 1 roce z deseti (90% VaR) by u dané investice s poměrem sm.odch./průměr 40 % ztratil více než cca. 40 % (inkasoval by 60 po investování 100 na začátku roku).
Výše uvedené je přirozeně jednoduchým případem, dobrým tak pro rychlý odhad rizikovosti jednoduché investice. I když princip odhadu VaR je stejný i pro komplexní investiční portfolia, potíž leží v kvantifikaci vstupních proměnných díky vzájemné interakci jednotlivých složek portfolia - např. akcií, call/put opcí, atd. Příště se podíváme na to zda, popř. nakolik je tento koncep využitelný při posuzování atraktivnosti reálných investic - akvizic, výrobních technologií, brandingu, atd.