Včera jsme se tu věnovali tomu, že u utilit dosahuje rozdíl mezi dividendovými výnosy a výnosy vládních dluhopisů dost nízkých hodnot – utility nejsou z tohoto pohledu nijak levné. Podobné srovnávání dividendových, či ziskových výnosů akcií s výnosy dluhopisů je přitom dost časté, občas se mu věnuji i já. A dnes bych rád zabrousil do trochu techničtější části celé věci. Která ale osvětlí pár zajímavých věcí, relevantní i při změnách inflačních režimů.
V následujících dvou tabulkách první čtyři proměnné určují férovou hodnotu valuací, tedy poměr cen k ziskům PE. Předposlední sloupec pak ukazuje obrácené PE, nazývané často ziskový výnos akcií. A poslední sloupec je vrcholem dnešního příběhu čísel a slov, jde o rozdíl mezi oním ziskovým výnosem a bezrizikovými sazbami Rfr. Těmi jsou výnosy desetiletých vládních dluhopisů, které spolu s rizikovou prémií akciového trhu RP, očekávaným dlouhodobým růstem zisků G a poměrem dividend k ziskům POR určují ono férové PE.
Ono férové PE je na základě Gordonova růstového vzorce rovno POR dělenému rozdílem mezi požadovanou návratností a růstem. Požadovaná návratnost je přitom dána bezrizikovými výnosy a rizikovou prémií. Dvě tabulky se pak liší v jednom důležitém aspektu – v první jsou od sebe odtržené výnosy dluhopisů a růst ekonomiky/zisků, v druhé se tyto dvě proměnné kopírují.
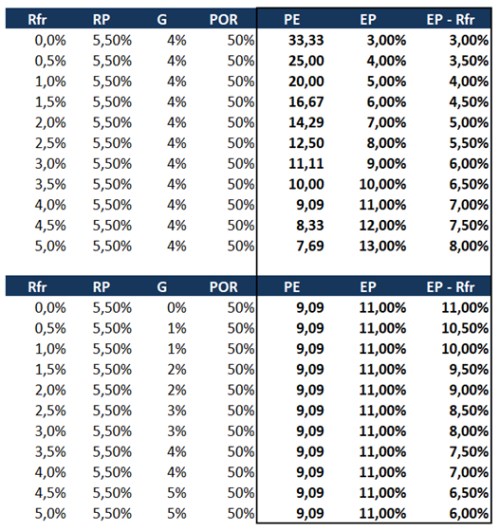
První tabulka tedy modeluje situaci, kdy se výnosy dluhopisů mění relativně k očekávanému růstu. Výsledek je intuitivní – čím níže jsou výnosy relativně k růstu, o to nižší je celková požadovaná návratnost relativně k růstu a o to vyšší jsou valuace (PE). EP naopak klesá a klesá i rozdíl mezi ním a výnosy dluhopisů – poslední sloupec. Ten se tedy mění i přesto, že riziková prémie akciového trhu je stále stejná (5,5 %). Vidíme tu tedy na konkrétních číslech a výpočtech, že navzdory občasným tvrzením tento rozdíl není prémií, ale obsahuje v sobě prémie i očekávaný růst. A mění se tudíž i v případě, že prémie jsou konstantní.
Druhá tabulka by měla být realističtější, protože výnosy dlouhodobých dluhopisů by měly být výrazně ovlivněny růstově-inflačním výhledem. Zde tedy konkrétně platí předpoklad, že při růstu ekonomiky/zisků o 1 % jsou výnosy na 1 % atd. Takové provázání pak znamená, že PE se při změnách růstu/výnosů nemění a to samé pak platí o EP. Mění se ale rozdíl mezi EP a výnosy a to v opačném směru, než v tabulce první: Pokud výnosy rostou (kvůli vyššímu tempu růstu ekonomiky a zisků), rozdíl mezi EP a výnosy dluhopisů se snižuje. Opět zde přitom platí, že rizikové prémie jsou konstantní a rozdíl opět neukazuje jejich výši, ale míchá jí s růstem. Navíc se ale ukazuje jedna podstatná věc:
Valuace (PE) mohou být při změnách výnosů/růstu stále na svých férových úrovních, ale rozdíl mezi EP a bezrizikovými sazbami se může výrazně měnit. Či řečeno obráceně: Pokud jsou výnosy provázány s růstem, změny rozdílu mezi EP a výnosy nemusí ukazovat na odchylku od férových valuací. Je totiž dána čistě matematicky. Připomeňme si v této souvislosti včerejší graf, kde je rozdíl mezi dividendovými výnosy utilit a výnosy dluhopisů. V principu u něj platí to samé a vidíme, že rozdíl se v období velmi nízkých sazeb pohyboval výš, než nyní, kdy jsou sazby výrazně výš. To je mustr popsaný druhou tabulkou:
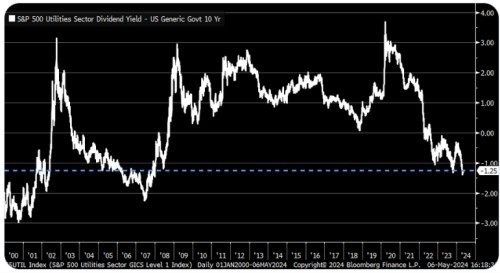
Zdroj: X
Krátké suma sumárum: Rozdíl mezi obráceným PE a výnosy dluhopisů není rizikovou prémií akciového trhu. A jeho změny probíhající při změnách výnosů dluhopisů mohou být alespoň z části čistě matematického rázu. A nemusí moc říkat o odchylkách od férových valuací, míře nadhodnocenosti, či podhodnocenosti trhu. Při relativně malých změnách sazeb je tento efekt méně významný, ale pokud se mění ekonomické, inflační a sazbové režimy, může tomu být jinak. Praxe je pak pestřejší – může ležet někde mezi první a druhou tabulkou, mění se i prémie a POR a růst zisků se může výrazně odchylovat od růstu ekonomiky.