Ke konci roku tu obvykle píšu nějaké uvolněnější věci, minulý týden jsem ale tuto tradici porušil. Chtěl jsem dotáhnout do určitého konce sérii článků týkajících se predikcí pro rok letošní. Ono uvolněnější téma jsem si nechal pro začátek roku - vyjasněme si radši hned pár klíčových věcí...
Před týdnem jsem poukazoval na to, že podle trhů Fed zvedne sazby nejpozději do března s 63% pravděpodobností. Není to přitom tak dávno (konec září), co byla tato pravděpodobnost hodnocena jako v podstatě nulová. Nyní se sazby nachází na 0 % (přesně je to 0,08 %) a dejme tomu, že Fed je v březnu zvedne o 0,25 procentního bodu a v červnu o dalších 0,25 procentního bodu. Budou tak dosahovat 0,5 %. A budou dvakrát vyšší než v březnu. Nebo jednou tak vyšší?
Podobně můžeme narazit ve chvíli, kdy hodnotíme řadu dalších čísel, včetně cen akcií. Vzrostly akcie Tesly od konce roku 2020 jednou tolik, nebo dvakrát tolik (z 530 na 1060 dolarů)? A dejme tomu, že by někdo četl nějakou investiční analýzu, podle které by trh měl letos posílit jednou tolik jako v minulém roce. Pro matematika nepřipouštějícího jazykové nuance by to asi znamenalo, že trh si připíše zisky stejné, protože třeba 1 krát 10 % je 10 %. Na to bychom ale asi namítli, že pokud bychom chtěli vyjádřit stejnou návratnost, tak asi nebude používat výraz jednou tolik. A na to se zase nabízí námitka, kolik by tedy bylo dvakrát tolik, když jednou tolik by bylo skutečně 20 %.
Mně asi nejvíce sedí pohled, podle kterého se „jednou tolik“ točí kolem sčítání, zatímco „dvakrát tolik“ a všechny další „toliky“ už kolem násobení. Zisky „jednou tolik“ jsou tedy zisky ve výši 10 % plus 10 %, tedy 20 %. A zisky „dvakrátolikové“ jsou 10 % krát 2, tedy také 20 %. Nesmíme ale začít operovat s dodatky typu „ještě“. Pak se nám i „dvakrát tolik“ změní z násobícího režimu na sčítací a jsme ne na 20 %, ale na 30 %. Nejsystematičtější by asi bylo, pokud bychom nepoužívali „jednou tolik“ a brali vše jako násobení. K tomu asi ale nedojdeme. Vznik tohoto úsloví přitom podle některých jazykovědců pochází z doby, kdy lidé při obchodech nedovedli moc násobit, ale sčítání už jim šlo (jednou tolik = ještě jednou to samé).
Mimochodem stejně jako jednou a dvakrát toliky nás může zarážet třeba takové rčení „jeden za osumnáct a druhý bez dvou za dvacet“. Alespoň já jsem jej nikdy nechápal a to z prostého důvodu. Pokud je druhý bez dvou za dvacet (x – 2 = 20), tak je za 22. Úsloví snažící se vyjádřit totožnost obou tak vyjadřuje pravý opak. Pokud by to mělo dávat smysl, museli bychom použít formulaci „druhý za dvacet bez dvou“, či něco jako „druhému chybí dva do dvaceti“.
Proč je důležité vyjasnit si podobné věci ukazuje třeba následující graf. Ukazuje standardizované chování dolaru kolem prvního zvýšení sazeb americkou centrální bankou:
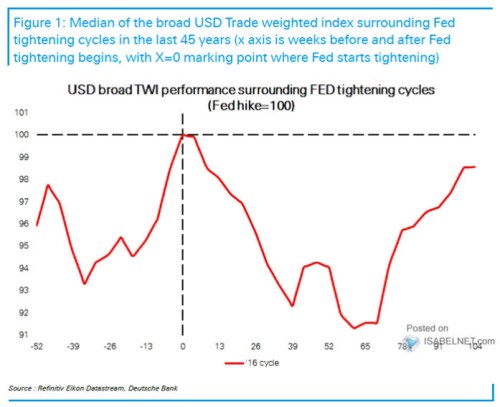
Vidíme, že téměř 40 týdnů před růstem sazeb dolar posiluje, následujících cca 40 týdnů ale ztrácí tolik, kolik předtím získal (je na stejné pozici jako na počátku). „Matematicky“ bychom také teoreticky mohli říci ztratil „jednou tolik“, protože násobení jednou s číslem nic neudělá. Jenže asi bychom to i přes jasnou matematiku vnímali tak, že jeho ztráty by byly dvojnásobné. Do násobících matematických výrazů bychom se tedy nepouštěli, protože bychom opět věděli, že u „jednou“ se sčítá, nenásobí. A mimochodem, pokud by Fed skutečně zvedl sazby již na počátku roku a dolar se choval podle onoho standardního mustru, šlo by to proti řadě předpovědí jeho pokračujícího posilování.