Investor, narozdíl od spekulantů, posuzuje své výnosy vždy v kontextu rizika, které podstoupil. Předpoklad přímé úměry mezi rizikem a požadovaným výnosem je přitom, zdá se, aplikovatelný pro většinu lidí, a to alespoň je-li velikost investice nezanedbatelná ve srovnání s jejich celkovým majetkem. Existuje přitom několik konceptů, jak hodnotit úspěšnost investora. Ty hlavní prezentujeme níže, s cílem upozornit na to, že i hodnocení investic v rámci podstoupeného rizika je principem jednoduchým, ovšem se značným prostorem pro variaci v praktickém uplatnění.
Výnos
Výnos je obecně souhrn všech finančních prostředků, které investorovi nebo firmě „vynesla“ jejich činnost. U investice je výnos odměnou za realizaci investice a měří se výnosovou mírou.
Výnosová míra je definována jako poměr peněz, které investice přinesla nebo prodělala, relativně ke své počáteční hodnotě – a je tedy vyjádřena v procentech. Úspěšnost investice lze posuzovat zpětně tzv. historickou výnosovou mírou; při rozhodování, zda investici realizovat, hodnotíme očekávanou výnosovou míru.
Historická výnosová míra
Příkladem vzorce pro výnosovou míru investice drženou po určité období je:
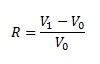
kde V0 je hodnota investice na začátku sledovaného období a V1 je její hodnota na konci sledovaného období. Pokud je investice držena více let – například tři roky - a my chceme zjistit takzvanou anualizovanou výnosovou míru – tedy o kolik procent narostla (poklesla) hodnota naší investice ročně (a ne za celé několikaleté období), použijeme vzorec:
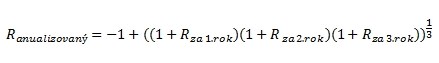
Obecný vzorec je tedy:

kde Ri je výnosová míra za rok i a n je celkový počet let, po které byla investice držena.
Očekávaná výnosová míra
Prvním krokem při určení očekávané výnosové míry je definovat, jaké výnosové míry mohou nastat, a následně jim přiřadit pravděpodobnost, s jakou mohou nastat.
Příkladem může být investice, u níž očekáváme čtyři možné situace: ztrátu 10 % s pravděpodobností 10 %, ztrátu o 5 % s pravděpodobností 10 %, zisk 10 % s pravděpodobností 50 % a zisk 20 % s pravděpodobností 30 %.
Tento proces samozřejmě zahrnuje velkou dávku subjektivity, je ovšem možné získat sofistikovanější odhady v závislosti na předchozích výnosech zvažované investice a výnosů srovnatelných investic. Do odhadů by se také měly zahrnout všeobecné tržní a ekonomické faktory, které by mohly úspěšnost investice ovlivnit.
Očekávaná výnosová míra se následně určí jako:
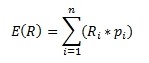
kde Ri je možná výnosová míra i a pi je pravděpodobnost této výnosové míry
V našem případě:
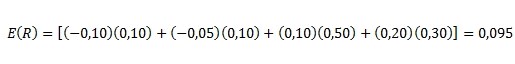
Očekávaná výnosová míra je tedy 9,5 %.
Výnos portfolia
Historická výnosová míra portfolia je součtem výnosových měr jednotlivých investic relativně k jejich podílu v portfoliu:
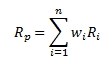
kde Ri je výnosová míra investice i, wi je váha (podíl) investice i v portfoliu a n je celkový počet investic (př. cenných papírů) v portfoliu
Očekávaná výnosová míra portfolia je analogicky součtem:
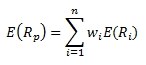
kde E(Ri) je očekávaná výnosová míra jednotlivé investice i, wi je váha (podíl) investice i v portfoliu a n je celkový počet investic (př. cenných papírů) v portfoliu.
Tržní likvidita
Tržní likvidita je možnost koupit nebo prodat aktivum rychle za aktuální cenu. I tzv. nelikvidní finanční aktiva se sice v mnoha případech dají rychle prodat nebo nakoupit, ale cena pak výrazně neodpovídá aktuální ceně. Pokud pak investor trvá na určité ceně, transakce může trvat mnohonásobně déle.
U cenných papírů se likvidita určuje několika způsoby. Jedním z nich je ukazatel trading turnover, který ukazuje, s kolika procenty určitých cenných papírů na trhu se opravdu obchodovalo. Je to tedy indikátor relativní tradingové aktivity a počítá se jako:

Obecně se za jeden z nejlikvidnějších trhů považuje americká burza, příkladem likvidního cenného papíru je např. Walgreens:
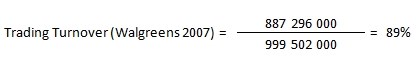
Dalším ukazatelem likvidity může být takzvaný rozdíl mezi poptávanou a nabízenou cenou (bid-ask spread) – čím nižší rozdíl, tím vyšší likvidita daného cenného papíru.
Riziko
Teorie předpokládá, že investoři jsou tzv. rizikově averzní – v případě, že mají na výběr dvě investice se stejnou úrovní výnosu, vyberou si vždy tu, která s sebou nese menší riziko. Jak se ale riziko měří?
Nejznámějším a nejpoužívanějším měřítkem rizika je rozptyl nebo standardní odchylka (přičemž standardní odchylka je pouze druhá odmocnina rozptylu). Rozptyl výnosové míry pro jednotlivé investice se počítá následovně:
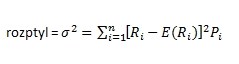
kde Ri jsou výnosy, které mohou nastat s pravděpodobností Pi, E(Ri) jsou očekávané výnosové míry ( střední hodnota). Standardní odchylka je pak:
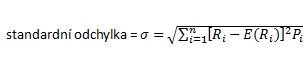
Riziko portfolia
V praxi ovšem investor nevlastní pouze jednu akcii, dluhopis nebo jiné finanční aktivum, ale kombinaci různých aktiv – takzvané portfolio. Jak moc je jeho portfolio rizikové, pak už ale nezávisí pouze na odchylce od očekávaných výnosů jednotlivých investic v portfoliu, ale také na tom, do jaké míry spolu výnosové míry jednotlivých investic souvisí. Měřítkem toho, do jaké míry se výnosy dvou investic pohybují ve stejném směru, je kovariance výnosů. Kladná kovariance znamená, že výnosy daných dvou investic mají ve stejném časovém úseku tendenci pohybovat se ve stejném směru – když roste jedna, roste druhá. Pokud je kovariance menší než nula, výnosy daných investic se pohybují v opačném směru (relativně vůči jejich středním hodnotám). Pokud jsou výnosy daných investic (v daném časovém období) na sobě nezávislé, je kovariance rovna nule.
Pro dvě investice (aktiva) i a j definujeme kovarianci výnosových měr následovně:
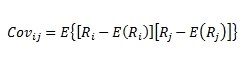
přičemž [Ri-E(Ri)] je odchylka výnosu investice i od její střední hodnoty a [Rj-E(Rj)] je odchylka výnosu investice j od její střední hodnoty. Covij je pak střední hodnota součinu těchto dvou odchylek.
Riziko portfolia se pak počítá s využitím kovariance následovně:
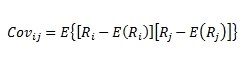
kde wi a wj je váha investice i a j v portfoliu (váhy jsou dány proporcí hodnoty investice v hodnotě portfolia), ?i2 je rozptyl výnosových měr investice i a Covij je kovariance mezi výnosovými mírami investice i a j.
Návratnost a riziko
CAPM - dobrý začátek
Zřejmě nejpoužívanějším konceptem kvantifikujícím vztah mezi požadovanou mírou návratnosti a rizikem akcie je CAPM, založený na teorii portfolia. Jeho klíčovým ukazatelem je zde již několikrát diskutovaná beta (indikátor systematického rizika). Zopakujme, že v jeho rámci se požadovaná míra návratnosti rovná:
r = bezriziková sazba + beta*riziková prémie trhu
Následující graf demonstruje citlivost požadované míry návratnosti, kalkulované na základě výše uvedeného, na rozdílnou betu (osa x) a rizikovou prémii trhu (osa z, bezriziková sazba je orientačně na 5%), je patrné, že rozdílná volba těchto parametrů produkuje značně rozdílné výstupní hodnoty:

Zdroj: Patria Finance
Většina kritiky CAPM má svůj původ v tom, že samotná teorie portfolia je odvozena v rámci uzavřeného, neoklasického modelu ekonomiky, který je sice dobrým myšlenkovým rámcem pro posouzení určitých jevů v reálném světě, zdaleka ale není dostačující. Dobrým příkladem je rozdíl mezi rizikem a nejistotou.
Riziko je kvantifikovatelné (možnost odhadu pravděpodobností různých výstupů) a jako takové je vhodným vstupem do "mainstream" modelů. V praxi ho však lze pozorovat pouze v situacích, jako je např. hod kostkou, či ruleta. Většina budoucích jevů není předmětem rizika, ale nejistoty - odhady pravděpodobností výstupů jsou ve skutečnosti pouze intuitivně "nastřelenými" čísly. Pojem a koncept rizika je ale přesto široce rozšířený, což je zejména odrazem právě jeho relativně lehké použitelnosti v praktických a teoretických financích a ekonomii.
Beta
Beta, která ukazuje citlivost pohybu akcie na pohyb akciového trhu (z hlediska ekonomiky a výsledků společností pak indikuje citlivost jejich výsledků na ekonomický cyklus) je jedním z nejužívanějších konceptů v rámci valuace společností a investičního managementu.
Možné je rozdělení celkového rizika, kterému investor při investici do akcií čelí, na riziko systematické (reflektované v betě) a na nesystematické. Z pohledu investora můžeme konstatovat, že pouze systematické riziko je to, za které se platí zvýšenou návratností investice - nesystematické může být oddiverzifikováno. To je mimochodem jedním z hlavních důvodů, proč investiční doporučení brokerů, bank a jiných finančních institucí, založené na odhadu fundamentální hodnoty akcie za pomocí CAPM, nebo APT a bety (tj. akcie, která je součástí vysoce diverzifikovaného portfolia), není v žádném případě určeno pro investory investující pouze do jedné, či několika málo akcií.
Princip bety znázorňuje následující graf:
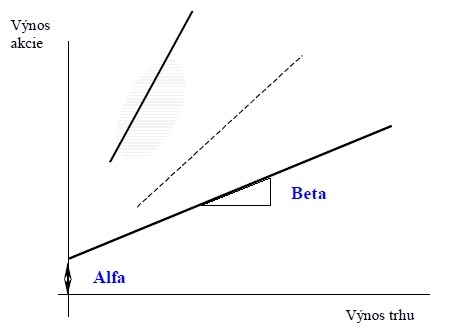
Zdroj: Patria Finance
Zde nejdříve připomeňme, že alfa vyznačená v grafu ukazuje, kolik je dle regresní přímky výnos akcie v případě nulového výnosu trhu; je naprosto rozdílným konceptem od Jensenovy alfy.
Mírně odbočme a poukažme nyní na jeden aspekt konceptu bety, který může rozšířit investiční analýzu určitého titulu. Tímto je rozdílná korelace mezi pohybem trhu a pohybem jednotlivých akcií - tj. nakolik regresní přímka v grafu vystihuje pohyb akcie v závislosti na pohybu trhu. Tato korelace tak určitým způsobem indikuje vypovídací schopnost bety - čím je korelace bližší jedné, o to „spolehlivěji“ se akcie pohybuje společně s trhem, a to se senzitivitou charakterizovanou betou. Korelaci lze také chápat jako indikaci nesystematického rizika - čím vyšší je, tím menší je nutnost diverzifikace (realizované výnosy jsou blíže k regresní přímce) a naopak. Pokud tak investor chce např. vsadit na oživení ekonomiky a investovat do akcií s vysokou betou (těch, které budou na toto oživení silně reagovat), bude si primárně vybírat ty sektory/společnosti, kde je zmiňovaná korelace vyšší.
Následující graf ukazuje, že spektrum možných korelací (data z jednotlivých odvětví USA) je široké, od velmi silné – blízké 1, až po velmi slabé -blízké nule. Z grafu je také patrná velice slabá závislost mezi korelací a betou samotnou. To mimo jiné indikuje malou sílu vztahu mezi velikostí rizika systematického (beta) a rizika nesystematického.
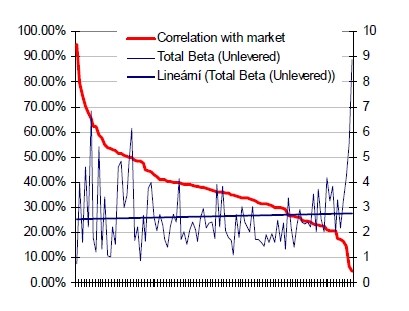
Zdroj: DamodaranOnline, Patria Finance
Odvození bety pro valuaci společnosti/akcie, popř. přímo pro samotné investiční rozhodnutí (např. zmiňovaná sázka na obrat ekonomického cyklu a na s tím korespondující více, či méně citlivé akcie) na základě historických dat (vývoj akcie a trhu) je pouze jednou z možností. Přestože má velikost bety pro určitou společnost v čase většinou relativně velkou setrvačnost, k jejím změnám např. v závislosti na vývoji daného odvětví (postupné nasycení trhu, zvyšující se konkurence, regulace atd.) a společnosti (nové produkty, inovace, technologie výroby, akvizice atd.) dochází – tj. senzitivita se mění. Pro odhad bety je proto vhodná kombinace pohledu do historie a zvážení hlavních faktorů v budoucnu působících na citlivost výsledků společnosti na pohyb trhů.
Ačkoliv se betě dá mnoho vytknout, jistou vypovídací schopnost o rizikovosti společnosti, či odvětví má. To se dá demonstrovat např. na oblíbeném tématu o optimální velikosti zadlužení společnosti. Na úrovni nejjednodušších teorií tato na hodnotu společnosti nemá žádný vliv (M&M I pro ty, kteří se o toto zajímají více), hlubší teorie a praxe reflektují vliv operačního rizika (fluktuace poptávky, tržeb a zisků) na riziko finanční a tudíž na finanční páku. To jednoduše řečeno znamená, že čím méně rizikové je dané odvětví z operačního pohledu, tím více může společnost využívat daňový štít pocházející z odpočitatelnosti úrokových nákladů z daňového základu (tj. tím více se zadlužuje).
Na tomto místě znovu připomeňme, že teze o lacinějším dluhu z pohledu nákladu financování je mýtus - čím větší proporce tohoto financování na celkovém kapitálu, tím větší je požadovaná míra návratnosti na jednotku vlastního jmění. Dluh může být výhodný pouze díky zmiňované odpočitatelnosti úroků.
Zpět k betě - následující graf ukazuje negativní závislost mezi betou a mírou zadlužení (poměr dluhu a vlastního jmění), potvrzující to, že čím více roste operační riziko, tím méně může (měla by) společnost využívat dluh k maximalizaci své hodnoty. V kontextu finančních teorií, čím větší operační riziko, tím dříve se při vzrůstajícím zadlužení objeví tzv. náklady bankrotu.
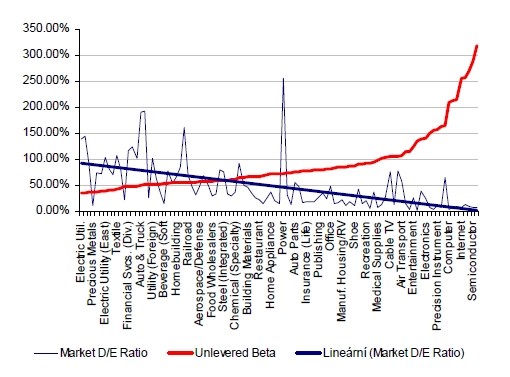
Zdroj:DamodaranOnline, Patria Finance
Multifaktorové modely
Kritika CAPM je do značné míry zaměřená na jeho nedostatečnou reflexi toho, že faktorů, které ovlivňují výnos akcie, je více, než její citlivost na trh a návratnost trhu. To dalo základ multifaktorovým modelům, jako je např. APT. Jejich principem je definice několika faktorů určujících návratnost akcií a určení citlivostí (bet) akcie na každý takový faktor.
Princip dvoufaktorového modelu (r = Rrf + beta1*RP1 + beta2*RP2) může představovat následující graf, na osách x a z jsou velikosti bet pro jednotlivé faktory (jejich rizikové prémie RP), na ose y požadovaná míra návratnosti r. CAPM přitom může být vnímán jako model pouze na osách x a y.

Zdroj:Patria Finance
Problémem v těchto případech je definice faktorů působících na návratnost akcie, určení jednotlivých velikostí bet a rizikových prémií pro každý faktor (prémie při dané betě rovné 1 a ostatních betách rovných 0).
Jaká je vaše alfa?
Výše uvedené tak implikuje jeden z možných pohledů na úspěšnost investora v dimenzích riziko-výnos. Toto je reflektované v tzv. Jensenově alfě, která je definována jako:
Alfa = návratnost investice (portfolia) - [Rrf + beta*MRP]
Nejde tedy o nic jiného, než o to, kolik investor vydělal nad, nebo pod, požadovanou míru návratnosti určenou za pomocí CAPM (alternativně APT).
Princip znázorňuje následující graf, ukazující návratnost a následně alfy dvou portfolií, jedno s alfou pozitivní a jedno negativní.

Zdroj: Patria Finance
Sharp ratio
Sharpův poměr je alternativním měřítkem úspěšnosti investora, která je v principu definovaná jako jeho dosažený výnos upravený o riziko. Ačkoliv princip rozdělení celkového rizika na systematické a nesystematické má elegantní teoretické zdůvodnění, není málo investorů, kteří minimálně berou v úvahu stále riziko celkové (tedy nejen jeho systematickou část). V principu by tak měli činit všichni, kteří nemají dobře diverzifikované portfolio alespoň z několika desítek akcií. Jim v hodnocení úspěšnosti svých investic, či spekulací může pomoci tzv. Sharpův poměr. Ten ukazuje, jaký byl výnos investora upravený o riziko, konkrétně výnos nad bezrizikovou investici dělený volatilitou jeho portfolia (jde o anualizované hodnoty, volatilita je anualizovaná denní standardní odchylka procentuálních změn hodnoty portfolia).
Hodnoty tohoto poměru v závislosti na návratnosti portfolia (osa z) a volatilitě (osa x) znázorňuje následující graf:

Zdroj: Patria Finance
Interpretace (tzn. posouzení úspěšnosti) výsledku investice na základě výše uvedeného poměru je samozřejmě silně subjektivní. Na základě zkušeností je ale někdy uváděno, že u neprofesionálních investorů je úspěchem překročení 1 (v delším období) - tzn. že návratnost portfolia nad bezrizikovou sazbu se rovná volatilitě.